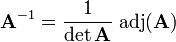Módulo 4. Sistemas de Ecuaciones Lineales y Matrices.
Objetivo Particular del Periodo:
El alumno entenderá los conceptos elementales del álgebra lineal y los aplicará en problemas del ámbito económico y de gestión de negocios.
Objetivo Particular del Periodo:
El alumno entenderá los conceptos elementales del álgebra lineal y los aplicará en problemas del ámbito económico y de gestión de negocios.
4.1 Sistemas de Ecuaciones Lineales.
Un sistema de ecuaciones lineales es un conjunto de expresiones algebraicas de la forma:
a11x1 + a12x2 + ....+a1nxn = b1
a21x1 + a22x2 + ....+a2nxn = b2
...........................................
am1x1 + am2x2 + ....+amnxn = bm
xi son las incógnitas, (i = 1,2,...,n).
aij son los coeficientes, (i = 1,2,...,m) (j = 1,2,...,n).
bi son los términos independientes, (i = 1,2,...,m).
aij y b i 
 .
.

 .
.
m, n 
 ;
;

 ;
;
m > n, ó, m = n, ó, m < n.
Obsérvese que el número de ecuaciones no tiene por qué ser igual al número de incógnitas.
Cuando n toma un valor bajo, es usual designar a las incógnitas con las letras x, y, z, t, ...
Cuando bi = 0 para todo i, el sistema se llama homogéneo.
4.1.1 Definición.
Una ecuación es una proposición que expresa la igualdad de dos expresiones algebraicas.
Por lo regular involucra una o más variables y el símbolo de igualdad, .
Las siguientes proposiciones son ejemplos de ecuaciones.
2x - 3 = 9 x (1)
y2 - 5y = 6 - 4y (2)
2x + y = 7 (3)
a/1-r = s (4)
4.1.2 Sistemas de Ecuaciones Lineales: Consistentes, Inconsistentes, y su representación paramétrica del conjunto solución.
Por lo general, hay tres posibilidades para un sistema de ecuaciones lineales: ninguna solución, una sola solución, o un número infinito de soluciones. Un sistema que tiene una o más soluciones se llama consistente. Si no hay soluciones, el sistema se llama inconsistente. Un sistema con menos ecuaciones que incógnitas se llamaindeterminado. Aquellos son los sistemas que frecuentemente tienen un número infinito de soluciones. Un sistema en que el número de ecuaciones excede el número de incógnitas se llama superdeterminado. En un sistema superdeterminado, cualquier cosa puede pasar, pero tal sistema es frecuentemente inconsistente.
Ejemplo
El sistema
| 2x | - | y | + | 3z | = | 0 |
| x | + | y | - | 3z | = | 1 |
es indeterminado y consistente con solución
- x = 1/3; y = 2/3 + 3z, z arbitraria.
El sistema
| x | + | y | - | z | = | 4 |
| 3x | + | y | - | z | = | 6 |
| x | + | y | - | 2z | = | 4 |
| 3x | + | 2y | - | z | = | 9 |
es superdeterminado y consistente con una única solución
- x = 1, y = 3, z = 0.
4.1.3 Métodos para resolución de sistemas de ecuaciones lineales: método gráfico, igualación, sustitución, eliminación, (sumas y restas).
Una solución de una ecuación lineal con dos incógnitas x y y consiste en una pareja de números: un valor de x y un valor de y, que satisfacen la ecuación. En un sentido más amplio, una solución de un sistema de dos o más ecuaciones lineales es una solución que satisface a la vez todas las ecuaciones en el sistema.
Podemos resolver un sistema de ecuaciones lineales gráficamente, por dibujar las gráficas y determinar donde se cruzan, o algebráicamente, por combinar las ecuaciones para eliminar cada incógnita salvo que una, y entonces despejarla.
Un sistema de dos ecuaciones lineales tiene:
(1) Una sola (única) solución. Ocurre este caso cuando las dos rectas correspondientes no están paralelas, y entonces se cruzan en un solo punto.
(2) Ninguna solución. Ocurre este caso cuando las dos rectas son paralelas y distintas.
(3) Un número infinito de soluciones. Ocurre este caso cuando las dos ecuaciones representan la misma recta. En este caso, se represente las soluciones por designar una variable como arbitraria y despejar a la otra.
El sistema
| 2x - y | = | 0 |
| x + y | = | 1 |
El sistema
| 2x - y | = | 0 |
| 4x - 2y | = | 1 |
El sistema
| x - y | = | 2 |
| -2x + 2y | = | -4 |
- x = 2 + y, y arbitraria.
4.1.4 Sistemas de Ecuaciones Equivalentes.
Los sistemas de ecuaciones equivalentes son los que tienen el mismo conjunto de soluciones, aunque tengan distinto número de ecuaciones.
Obtenemos sistemas equivalentes por eliminación de ecuaciones dependientes. Si:
- Todos los coeficientes son ceros
- Dos ecuaciones son iguales.
- Una ecuación es proporcional a otra.
- Una ecuación es combinación lineal de otras.
4.1.5 Eliminación de Gauss y Gauss-Jordan.
El método de Gauss consiste en transformar un sistema de ecuaciones en otro equivalente de forma que éste sea escalonado.
Obtenemos sistemas equivalentes por eliminación de ecuaciones dependientes. Si:
- Todos los coeficientes son ceros.
- Dos filas son iguales.
- Una fila es proporcional a otra.
- Una fila es combinación lineal de otras.
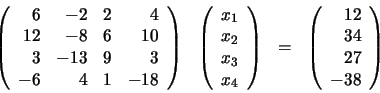
Método de Eliminación de Gauss-Jordan.
Supongamos que es necesario encontrar los números "x", "y", "z", que satisfacen simultáneamente estas ecuaciones:
Esto es llamado un sistema lineal de ecuaciones. El objetivo es reducir el sistema a otro equivalente, que tenga las mismas soluciones. Las operaciones (llamadas elementales) son estas:
- Multiplicar una ecuación por un escalar no nulo.
- Intercambiar de posición dos ecuaciones
- Sumar a una ecuación un múltiplo de otra.
Estas operaciones pueden representarse con matrices elementales que se usan también en otros procedimientos como la factorización LU o la diagonalización por congruencia de una matriz simétrica.
En nuestro ejemplo, eliminamos x de la segunda ecuación sumando 3/2 veces la primera ecuación a la segunda y después sumamos la primera ecuación a la tercera. El resultado es:
Ahora eliminamos y de la primera ecuación sumando -2 veces la segunda ecuación a la primera, y sumamos -4 veces la segunda ecuación a la tercera para eliminar y.
Finalmente eliminamos z de la primera ecuación sumando -2 veces la tercera ecuación a la primera, y sumando 1/2 veces la tercera ecuación a la segunda para eliminar z.
Despejando, podemos ver las soluciones:
Para clarificar los pasos, se trabaja con la matriz aumentada. Podemos ver los 3 pasos en su notación matricial:
Primero:
Después,
Por último.
Si el sistema fuera incompatible, entonces nos encontraríamos con una fila como esta:
Que representa la ecuación: 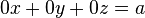 , donde a ≠ 0. Es decir,
, donde a ≠ 0. Es decir, 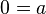 , lo que supone una contradicción y, por tanto, no tiene solución.
, lo que supone una contradicción y, por tanto, no tiene solución.
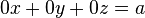 , donde a ≠ 0. Es decir,
, donde a ≠ 0. Es decir, 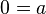 , lo que supone una contradicción y, por tanto, no tiene solución.
, lo que supone una contradicción y, por tanto, no tiene solución.
4.1.5.1 Definición de Matriz.
Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas.

4.1.5.2 Expresión Matricial de un Sistema de Ecuaciones Lineales.
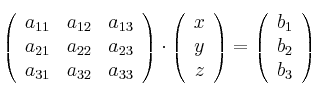





![\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-b4daf9b08947470816a091c908c8b878.png)
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-9d6156e83361678f19df40db3ecf5638.png)
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-45eb9fde313d2a75f1b05cd42aac6c52.png)
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-0730ab56aabea929252d49dbf9595acc.png)
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-eb6ec9bc0f3d4f3655e297c2d80271fe.png)
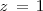
En la primera y segunda ecuación, sustituimos por la solución de la tercera ecuación (
por la solución de la tercera ecuación ( 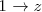 ), para obtener:
), para obtener:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-5c98a4989cffb856e694abe6316e1767.png)

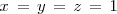









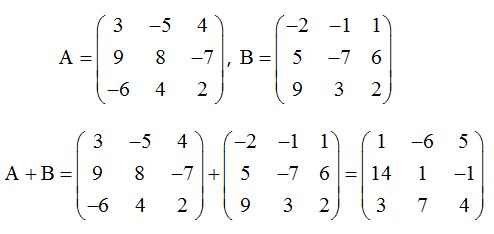











 F3 = F1 + F2
F3 = F1 + F2









 Sustitución
Sustitución
 Igualación
Igualación
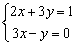
 Reducción
Reducción
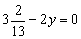 y =3/13
y =3/13
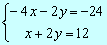 sumando –3x= -12Þ x =4
sumando –3x= -12Þ x =4
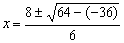 =
=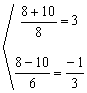
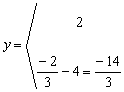
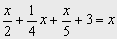
 A ½ B
A ½ B
 Al igualar los tiempos empleados por ambas, se obtiene:
Al igualar los tiempos empleados por ambas, se obtiene:
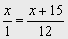 Þ 12x =x +15Þx =15/11= 1minuto 21segundos
Þ 12x =x +15Þx =15/11= 1minuto 21segundos
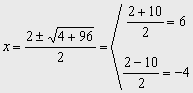
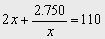 Þ 2x2+1500 =110 x Þ 2x2-110x +1500=0
Þ 2x2+1500 =110 x Þ 2x2-110x +1500=0
Dado un sistema de ecuaciones
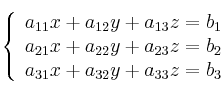
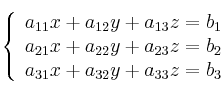
Se puede expresar de forma matricial de la siguiente manera:
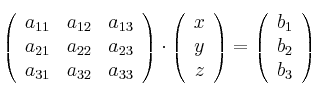
La expresión anterior, de forma abreviada 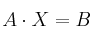 , se llama expresión matricial del sistema. Las matrices se conocen como:
, se llama expresión matricial del sistema. Las matrices se conocen como:

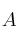 matriz de los coeficientes
matriz de los coeficientes

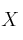 matriz de las incógnitas
matriz de las incógnitas

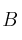 matriz de los términos independientes
matriz de los términos independientes
Hay 3 operaciones básicas usadas en los renglones de una matriz cuando está usando la matriz para resolver un sistema de ecuaciones lineales. El objetivo usualmente es conseguir que la parte izquierda de la matriz se parezca a la matriz identidad.
Las tres operaciones son:
- Cambiar renglones
- Multiplicar un renglón por un número
- Sumar renglones
Cambio de renglones
Puede cambiar los renglones de una matriz para obtener una matriz nueva.

En el ejemplo anterior mostrado, movimos el Renglón 1 al Renglón 2, el Renglón 2 al Renglón 3, y el Renglón 3 al Renglón 1. (La razón para hacer esto es conseguir que el 1 esté en la esquina superior izquierda.)
Multiplicar un renglón por un número
Puede multiplicar cualquier renglón por un número. (Esto significa multiplicar cada entrada en el renglón por el mismo número.)

En este ejemplo, hemos multiplicado el Renglón 3 de la matriz por 1/3. (Esto nos arroja el 1 que necesitamos en el Renglón 3, Columna 3.)
Sumar renglones
También puede sumar dos renglones juntos, y reemplazar un renglón con el resultado.
Por ejemplo, en la matriz que resultó del último ejemplo, podemos sumar los renglones 2 y 3 juntos, entrada por entrada:

Luego, reemplazamos el Renglón 2 con el resultado.

4.1.5.4 Reducción de Gauss y Gauss-Jordan.
El método de Gauss consiste en transformar el sistema dado en otro equivalente. Para ello tomamos la matriz ampliada del sistema y mediante las operaciones elementales por filas la transformamos en una matriz triangular superior ( o inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil de resolver.
Ejemplo
La matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-b4daf9b08947470816a091c908c8b878.png)
es:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-9d6156e83361678f19df40db3ecf5638.png)
Si a la tercera y segunda fila le restamos la primera, obtenemos:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-45eb9fde313d2a75f1b05cd42aac6c52.png)
Si ahora intercambiamos la segunda y tercera filas, obtenemos
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)](http://www.wikillerato.org/images/math/math-0730ab56aabea929252d49dbf9595acc.png)
que es la matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-eb6ec9bc0f3d4f3655e297c2d80271fe.png)
que es equivalente al inicial.
Solucionamos la tercera ecuación para obtener  :
:
 :
: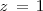
En la primera y segunda ecuación, sustituimos
 por la solución de la tercera ecuación (
por la solución de la tercera ecuación ( 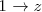 ), para obtener:
), para obtener:![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.](http://www.wikillerato.org/images/math/math-5c98a4989cffb856e694abe6316e1767.png)
La segunda ecuación es ahora una ecuación con una sola incógnita,  , que resolvemos para obtener
, que resolvemos para obtener 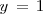 . Sustituimos, en la primera ecuación,
. Sustituimos, en la primera ecuación,  por 1 (
por 1 ( 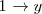 ). Esto nos da una ecuación en
). Esto nos da una ecuación en  :
:
 , que resolvemos para obtener
, que resolvemos para obtener 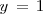 . Sustituimos, en la primera ecuación,
. Sustituimos, en la primera ecuación,  por 1 (
por 1 ( 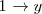 ). Esto nos da una ecuación en
). Esto nos da una ecuación en  :
:
que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
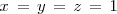
4.1.5.5 Sistemas homogéneos.
Llamamos sistema de ecuaciones a un conjunto cualquiera de ecuaciones. Por ejemplo, las ecuaciones:

forman un sistema de dos ecuaciones con dos incógnitas.
El conjunto de ecuaciones:

forman un sistema de tres ecuaciones con tres incógnitas.
Se llama grado del sistema de ecuaciones al mayor exponente al que se encuentre elevada alguna incógnita del sistema.
Por ejemplo,

es un sistema de dos ecuaciones con dos incógnitas de segundo grado, porque el mayor exponente es 2 (la x e y al cuadrado). Este sistema con ecuaciones de segundo grado se llaman también sistema de ecuaciones cuadráticas.
El sistema de ecuaciones es de primer grado con dos incógnitas (porque todos los valores están elevados a 1, que no se escribe).
es de primer grado con dos incógnitas (porque todos los valores están elevados a 1, que no se escribe).
El sistema de ecuaciones
Cuando el sistema de ecuaciones es de primer grado y además no aparecen términos con las incógnitas multiplicadas entre sí(tipo x • y) se dice que es un sistema de ecuaciones lineales.
La matriz unidad de orden n×n es la matriz I de orden n×n en la cual todas las entradas son cero excepto los de la diagonal principal, que son 1. En símbolos:
- Iij = 1 si i = j y Iij = 0 si i ≠ j.
Una matriz cero es una matriz O en la cual todas las entradas son cero.
Las operaciones de adición, multiplicación escalar, multiplicación entre matrices se cumplen las siguientes reglas:
| A+(B+C) = (A+B)+C | Regla asociativa de adición |
| A+B = B+A | Regla conmutativa de adición |
| A+O = O+A = A | Regla unidad de adición |
| A+( - A) = O = ( - A)+A | Regla inversa de adición |
| c(A+B) = cA+cB | Regla distributiva |
| (c+d)A = cA+dA | Regla distributiva |
| 1A = A | Unidad escalar |
| 0A = O | Cero escalar |
| A(BC) = (AB)C | Regla asociativa de multiplicación |
| AI = IA = A | Regla unidad de multiplicación |
| A(B+C) = AB + AC | Regla distributiva |
| (A+B)C = AC + BC | Regla distributiva |
| OA = AO = O | Multiplicación por matriz cero |
| (A+B)T = AT + BT | Trasposición de una suma |
| (cA)T = c(AT) | Trasposición de un producto escalar |
| (AB)T = BTAT | Trasposición de un producto matriz |
La única regla que está notablemente ausente es la de conmutatividad del producto entre matrices. El producto entre matrices no es conmutativo: AB no es igual a BA en general.
Ejemplos
La siguiente es la matriz unidad de orden 4×4:
| I = |  |  | ||||
El fallo de la regla conmutativa para el producto entre matrices se muestra por el siguiente ejemplo:
| B = |
|
| AB = |
| ||||||
| BA = |
|
4.2.1 Tipos de matrices (cuadrada, rectangular,
triangular, matriz, identidad, matriz transpuesta).
Matriz fila
Una matriz fila está constituida por una sola fila.

Matriz columna
La matriz columna tiene una sola columna

Matriz rectangular
La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn.

Matriz traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.

(At)t = A
(A + B)t = At + Bt
(α ·A)t = α· At
(A · B)t = Bt · At
Matriz nula
En una matriz nula todos los elementos son ceros.

Matriz cuadrada
La matriz cuadrada tiene el mismo número de filas que de columnas.
Los elementos de la forma aii constituyen la diagonal principal.
La diagonal secundaria la forman los elementos con i+j = n+1, siendo n el orden de la matriz.

4.2.2 Operaciones con matrices (suma, diferencia,
multiplicación por escalar y producto de matrices).
Sumar y restar matrices
Para sumar y restar matrices, éstas pueden ser, las dos cuadradas o las dos rectangulares. El número de filas y columnas de una han de ser igual al número de filas y columnas de la segunda.
Sumar:
Sumamos los valores que ocupan la misma posición.
El valor que se halla en la posición (1 1) de A con el valor de la posición (1 1) de la matriz B.
El valor que se halla en la posición (1 2) de A con el valor de la posición (1 2) de la matriz B.
El valor que se halla en la posición (1 3) de A con el valor de la posición (1 3) de la matriz B. De este modo haremos con el resto de las filas.
Vamos a sumar las matrices A y B:
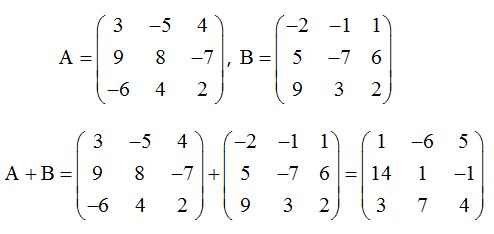
Restar matrices:
Es lo mismo que en el caso anterior pero restando los valores que ocupan las mismas posiciones:
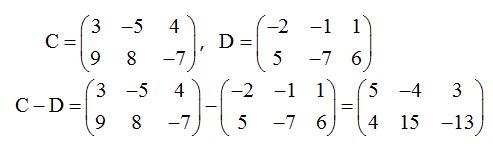
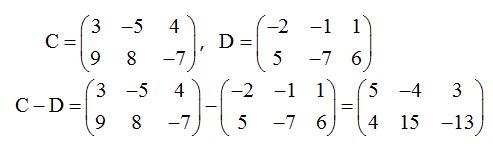
4.2.3 Propiedades de las operaciones con matrices.
1. Interna
La suma de dos matrices de orden m x n es otra matriz dimensión m x n.
2. Asociativa
A + (B + C) = (A + B) + C
3. Elemento neutro
A + 0 = A
Donde O es la matriz nula de la misma dimensión que la matriz A.
4. Elemento opuesto
A + (−A) = O
La matriz opuesta es aquella en que todos los elementos están cambiados de signo.
5. Conmutativa
A + B = B + A
4.2.4 Matriz inversa.
Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A−1, seguiremos los siguientes pasos:
1 Construir una matriz del tipo M = (A | I), es decir, A está en la mitad izquierda de M y la matriz identidad Ien la derecha.
Consideremos una matriz 3x3 arbitraria:

La ampliamos con la matriz identidad de orden 3.

2 Utilizando el método Gauss vamos a transformar la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: A−1.
F2 = F2 − F1

F3 = F3 + F2

F2 = F2 − F3

F1 = F1 + F2

F2 = (−1) F2

La matriz inversa es:

4.3 Determinantes.
A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A, denotado por |A| o pordet (A).
|A| = 

4.3.1 Definición de un determinante.
En el ámbito de la matemática, determinante es una expresión obtenida a partir de la aplicación de los elementos de una matriz cuadrada según ciertas reglas. Puede decirse que el determinante es una forma multilineal alternada.
4.3.2 Expansión por cofactores.
Dada una matriz cuadrada A, su matriz de adjuntos o matriz de cofactores cof(A) es la resultante de sustituir cada término aij de A por el cofactor aij de A. El término matriz adjunta adj(A) suele crear confusión, ya que en muchos tratados clásicos sobre álgebra lineal corresponde a la matriz de cofactorestraspuesta,1 2 3 sin embargo, en otros textos, se corresponde a la matriz de cofactores, puesto que llaman de la misma manera adjunto al cofactor y de ahí que sea adjunta.4 5 Aparte, también se utiliza el símbolo adj( ) indistintamente a cof( ) para el cálculo en los elementos de una matriz, haciendo, si cabe, la confusión más amplia.6
El interés principal de la matriz adjunta es que permite calcular la inversa de una matriz, ya que se cumple la relación:
donde adj(A^T) corresponde a la matriz de cofactores traspuesta, o sea,
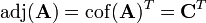 .
.
Sin embargo, para matrices de dimensiones grandes, este tipo de cálculo resulta más costoso, en términos de operaciones, que otros métodos como el método de eliminación de Gauss.
|At|= |A|
El determinante de una matriz A y el de su traspuesta At son iguales. 


2 |A| = 0 Si:
Posee dos filas (o columnas) iguales.

Todos los elementos de una fila (o una columna) son nulos.

Los elementos de una fila (o una columna) son combinación lineal de las otras.
 F3 = F1 + F2
F3 = F1 + F2
3 Un determinante triangular es igual al producto de los elementos de la diagonal principal.

4 Si en un determinante se cambian entre sí dos filas (o dos columnas), su valor sólo cambia de signo.



5 Si a los elementos de una fila (o una columna) se le suman los elementos de otra multiplicados previamente por un número real, el valor del determinante no varía.
Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.



6 Si se multiplica un determinante por un número real, queda multiplicado por dicho número cualquier fila (o cualquier columna), pero sólo una.

7 Si todos los elementos de una fila (o columna) están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes en los que las demás filas (o columnas) permanecen invariantes.

8 |A · B| =|A| · |B|
El determinante de un producto es igual al producto de los determinantes.
4.3.4 Regla de Cramer.
La regla de Cramer se aplica para resolver sistemas de ecuaciones lineales que cumplan las siguientes condiciones:
1 El número de ecuaciones es igual al número de incógnitas.
2 El determinante de la matriz de los coeficientes es distinto de cero.
Tales sistemas son sistemas compatibles determinados y se denominan sistemas de Cramer.

Sea Δ el determinante de la matriz de coeficientes.

Todo sistema de Cramer tiene una sola solución (es decir, es un sistema compatible determinado) que viene dada por las siguientes expresiones:

Δ1, Δ2 , Δ3, ... , Δn son los determinantes que se obtiene al sustituir los coeficientes del 2º miembro (los términos independientes) en la 1ª columna, en la 2ª columna, en la 3ª columna y en la enésima columna respectivamente.




Sistemas de ecuaciones lineales
Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales.
Ejemplo 16: 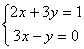 es un sistema de 2 ecuaciones con dos incógnitas
es un sistema de 2 ecuaciones con dos incógnitas
Resolver un sistema es encontrar la solución (o soluciones) común a todas ellas, o concluir que el sistema no tiene solución.
Hay tres métodos para resolverlos:
Ejemplo 17. 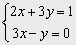
En la 2ª ecuación despejamos la y y la sustituimos en 1ª ecuación
y =3x; 2x +3(3x) =1Þ 11x =1
Þ x =1/11
Una vez encontrado el valor de una de las incógnitas se sustituye (y =3x) para encontrar el valor de la otra incógnita:
y =3/11
Observación. Este método es muy adecuado cuando el coeficiente de, al menos, una de las incógnitas es 1.
Ejemplo 18. Resuelve el sistema:
Despejamos la misma incógnita en las dos ecuaciones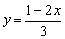 ; y =3x.
; y =3x.
Igualando 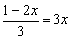 Þ 1-2x =9x Þ 1= 11x Þ x =1/11
Þ 1-2x =9x Þ 1= 11x Þ x =1/11
Ahora para obtener el valor de la y se procede como en el caso anterior, es decir se sustituye el valor hallado en la ecuación que más convenga
En este caso en y =3x, nos queda y =3/11
Observación. Este método es muy adecuado cuando el coeficiente de una de las incógnitas es igual en las dos ecuaciones.
Ejemplo 19. 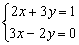
Multiplicamos la 1ª ecuación por 2 y la 2ª por 3. (De esta forma el coeficiente de y en las dos ecuaciones es el mismo, el m.c.m.
Resulta: 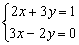 Þ
Þ 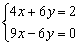
Sumando obtenemos 13 x =2 Þ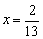
Sustituyendo el valor encontrado de x en la segunda ecuación:
Observación. Este método es muy adecuado en todos los casos.
Nota. A veces es más cómodo usar la reducción dos veces para encontrar el valor de la otra incógnita. (Ver ejercicio resuelto)
Ejercicios
Resuelve los siguientes sistemas por el método que creas más adecuado:
1) 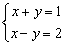
2) 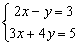
3) 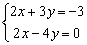
4)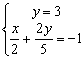
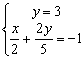
5) 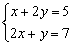
6) 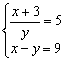
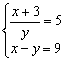
7)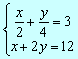
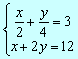
Solución
Para quitar los denominadores multiplicamos por 4 la 1ª ecuación Þ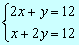
Le resolvemos por reducción doble.
Multiplicamos la 2ª ecuación por –2 Þ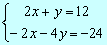
Sumando las dos ecuaciones obtenemos una equivalente: -3y = -12Þy =4
Para encontrar el valor de x, eliminamos la y, para ello multiplicando la 1ª por -2
8) 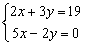
Problemas de aplicación
1) Calcula dos número cuya suma sea 8 y su producto 12.
2) La suma de dos número es 65 y su diferencia 23. Halla los números
3) La diferencia de dos números es 1/6. El triple del mayor menos el doble del menor es 1. Halla dichos números.
Sistemas de ecuaciones de 2º grado
Son aquellos en que al menos una de las ecuaciones es de 2º grado. Veremos con un ejemplo como proceder para obtener las soluciones
Ejemplo 20. Sea el sistema 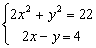
En la 2ª ecuación despejamos la y, y la sustituimos en la 1ª
y = 2x-4Þ 2x2+(2x –4)2=22
2x2 +4x2 –16x +16=22; 6x2-16x-6=0,
Simplificando por 2 obtenemos:3x2-8x-3=0, que es una ecuación de 2º grado completa:
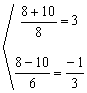
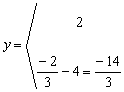
Ejercicios
Resuelve los siguientes sistemas:
1) 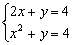
2) 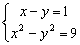
3)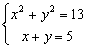
Para resolver un problema es conveniente realizar cuatro fases[1]:
1ª. Comprender el problema.
Hay que leer el problema hasta familiarizarse con él y que podamos contestar, sin dudar, a las siguientes preguntas:
¿Cuáles son los datos? ¿cuál es la incógnita o incógnitas? ¿son las condiciones suficientes para determinar a las incógnitas? ¿son insuficientes?.. .
2ª Concebir un plan.
Determinar la relación entre los datos y la incógnitas.
De no encontrarse una relación inmediata puedes considerar problemas auxiliares.
¿Conoces problemas relacionados con éste?
¿Podrías plantear el problema de forma diferente?
¿Puedes cambiar la incógnita o los datos o ambos si fuera necesario, de tal forma que la nueva incógnita y datos estén en una relación más sencilla?...
¿Has considerado todas las nociones esenciales del problema?
.................
Obtener finalmente un plan de solución.
Para nuestro caso:
Escribir la ecuación o ecuaciones que relacionan datos e incógnitas y analizar el sistema que forman.
3ª. Ejecutar el plan.
Resuelve el sistema por los métodos estudiados.
4ª. Examinar la solución obtenida.
Comprobar si las soluciones obtenidas son válidas y proceder en consecuencia.
Ejemplo 21.. Alejandra tiene 27 años más que su hija Carmen. Dentro de 8 años, la edad de Alejandra doblará a la de Carmen. ¿Cuántos años tiene cada una?
Solución. Sólo en este problema indicaremos con detalle las 4 fases
1º. Comprender el problema.
Es un problema con dos incógnitas y dos condiciones, luego suficientes para poder determinarlas.
Llamamos x a la edad de Alejandra e y a la de su hija.
Ordenamos los elementos del problema:
Hoy
|
dentro de 8 años
| |
La madre
|
x
|
x + 8
|
La hija
|
y
|
y + 8
|
2º. Concebir un plan.
Escribimos las ecuaciones que relacionan los datos con las incógnitas:
x = 27 + y
x + 8 = 2(y +8)
Es un sistema lineal de dos ecuaciones con dos incógnitas. Lo resolveremos por el método de sustitución.
3º Ejecutar el plan.
x = 27 + y
Entonces:
27 + y +8 = 2(y +8) de donde 35 -16 = y Þ y = 19, x = 46
4º Examinar la solución obtenida .
La solución obtenida es factible por ser entera.
El método empleado se puede usar en problemas “similares”.
Problemas resueltos
1. La edad de una madre es siete veces la de su hija. La diferencia entre sus edades es de 24 años. ¿qué edad tienen?.
Solución
Llamamos x a la edad de la hija, luego 7x será la edad de la madre.
7x –x =24Þ 6x =24 Þ x =4
Luego edad de la hija 4 años y edad de la madre 28 años
2. Halla un número tal que su mitad más su cuarta parte más 1, sea igual al número pedido.
Solución
Llamamos x al número que buscamos, la mitad del número es x/2 y su cuarta parte x/4
Entonces: 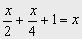
Multiplicamos por el m.c.m. que es 4. Nos queda:
2x +x + 4 = 4x
x =4
3. Se atribuye a Pitágoras la siguiente respuesta sobre el número de sus discípulos:
- Una mitad estudia matemáticas, una cuarta parte física, una quinta parte guarda silencio, y además hay tres mujeres.
¿Cuántos discípulos tenía?
Solución
Llamamos x al número de sus discípulos.
Traduciendo a lenguaje algebraico las condiciones, se tiene:
Multiplicando por 20, que es el m.c.m. , quitamos todos los denominadores
10x +5x +4x +60 =20x
Es decir, x = 60 discípulos
4. Dos poblaciones A y B distan 25km. Un peatón sale de A hacia B a una velocidad de 4km/h. Simultáneamente sale de B hacia A otro peatón a 6km/h. Calcula el tiempo que tardan en encontrarse.
Solución
25km
El espacio que recorre el peatón que sale de A es: E = v A t =4.t
El espacio que recorre el peatón que sale de B es: E = v B t = 6t
Cuando se encuentran habrán recorrido entre ambos los 25km
Por lo tanto: 4t +6t =25
10 t = 25 Þ t = 2,5 horas
Tardan en encontrarse 2 horas y media
5. En una jaula hay conejos y palomas, pueden contarse 35 cabezas y 94 patas. ¿Cuántos animales hay de cada clase?.
Solución
Llamamos x al número de conejos, y al número de palomas habrá entonces
x +y =35
Lo conejos tienen 4 patas, hay 4x patas de conejos
Las palomas 2 patas, luego tendremos 2y patas de palomas
El número de patas en total es 94 4x + 2y= 94Þ
Es decir 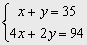 lo resolvemos por sustitución = y = 35 -x
lo resolvemos por sustitución = y = 35 -x
4x +2(35 –x) = 94
4x + 70 –2x =94
2x =24 Þ x =12 y =35 –12 =23
Hay 12 conejos y 23 palomas
6. Había doble de leche en un envase que en otro. Cuando se extrajeron 15 litros de leche de ambos envases, entonces había tres veces mas leche en el primer envase que en el segundo. ¿Cuánta leche había originariamente en cada envase.
Solución.
Llamamos x al nº de litros de un envase.
En el otro envase habrá 2x litros.
Al extraer 20 litros de cada envase nos quedan
x -15 2x –15
2x –15=3(x –15) =3x – 45
x =30
En un envase había 30 litros y en el otro 60 litros
7. El hermano mayor de una familia con tres hermanos tiene 4 años más que el segundo y éste 3 más que el menor. Si entre todos tienen la edad del padre que tiene 40 años ¿qué edad tiene cada hermano ?
Solución
Llamamos x = edad del hermano menor. Entonces según las condiciones del problema:
x + 3 es la edad del hermano mediano
x +3 + 4 = x + 7 es la edad del hermano mayor
Como la suma de las edades de los hermanos es 40:
x + x +3 + x +7 = 40 Þ 3x =40 –10 =30
x =10
Por lo tanto: edades de los tres hermanos: 10 , 13 y 17 años.
8. ¿ A qué hora forman por primera vez un ángulo rcto las agujas de un reloj, a partir del mediodía.
Solución
Es un caso particular de problemas de móviles.
La velocidad del minutero es doce veces mayor que la del horario. Podemos pues representar por 12 y 1 las velocidades respectivas de las dos saetas.
Si x es el nº de divisiones que ha recorrido la aguja horaria, la minutaría formará con ella ángulo recto cuando haya recorrido x +15 divisiones
 Al igualar los tiempos empleados por ambas, se obtiene:
Al igualar los tiempos empleados por ambas, se obtiene:
Se encuentran a las 12 horas 16 minutos 21 segundos
9. La edad de un padre es el cuadrado de la de su hijo. Dentro de 24 años la edad del padre será el doble de la del hijo. ¿Cuántos años tiene ahora cada uno?
Solución
Llamamos x a la edad del hijo. La del padre será x2
Dentro de 24 años el hijo tendrá x +24
Dentro de 24 años el padre tendrá x2 +24
Por lo tanto x2 +24 = 2(x +24) = 2x +48
La ecuación que resulta es de 2º grado.
x2- 2x –24=0
Por ser completa aplicamos la fórmula general:
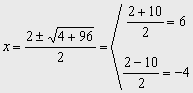
Aunque da dos soluciones, sólo la primera x =6 es válida, x =-4 no nos vale pues las edades no pueden ser negativas.
Por tanto el hijo tiene 6 años y el padre 36 años
10. Para vallar una finca rectangular de 750m2 se han utilizado 110m de cerca. Calcular las dimensiones de la cerca.
Solución
Llamamos x a la base del rectángulo, e y la altura.
Como la superficie es el producto de la base por la altura, entonces x .y =750
El perímetro es la suma de los 4 lados:
2x +2y =110
Es decir tenemos el sistema 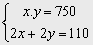 De la primera ecuación se tiene y =750/x
De la primera ecuación se tiene y =750/x
Sustituyendo en la segunda:
De donde 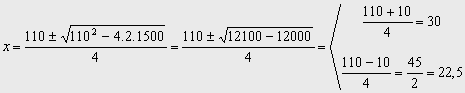
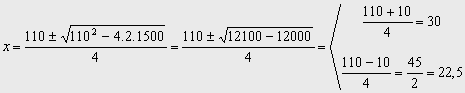
Nos da dos soluciones:
Si la base es x =30 Þ la altura es y = 750/30 =25
Si la base es x = 22,5 Þ la altura es y =750/22,5=100/3= 33,333..
Ambas válidas.
Conclusión:
Durante la última unidad de matemáticas aprendimos los diversos sistemas de ecuaciones lineales que existen, definimos el término, conocimos los sistemas de ecuaciones que hay, los métodos para poder resolver los sistemas de ecuaciones, los sistemas de ecuaciones equivalentes, el método de eliminación y de reducción de Gauss y de Gauss-Jordan; también aprendimos la definición de matriz, como se puede expresar una matriz en un sistema de ecuaciones, vimos las diferentes operaciones que se realizan en los renglones de las matrices, vimos los sistemas homógeneos; el álgebra de matrices, los tipos de matrices, las operaciones con las matrices, las propiedades de las operaciones con matrices, como obtener la matriz inversa y los determinantes, la definición de éstos, la expansión por cofactores, las propiedades de los determinantes, la regla de Cramer y como se pueden utilizar los sistemas de ecuaciones lineales con matrices en los diversos problemas como en el modelo de insumo-producto, análisis de ventas y los componentes del consumidor.
Bibliografía:
IES.
(2006). Expresión Matricial de un Sistema Lineal. 28/11/2015, de Matemáticasies
Sitio web: http://matematicasies.com/Expresion-matricial-de-un-sistema-lineal
Estudiia.
(2013). Expresión matricial de un sistema de ecuaciones lineales. 28/11/2015,
de Youtube Sitio web: https://www.youtube.com/watch?v=Xn6TVlj2ilE
Wforum.
(2012). Operaciones en renglones de matrices. 28/11/2015,
de Hotmath Sitio web: http://hotmath.com/hotmath_help/spanish/topics/matrix-row-operations.html
Unicoos.
(2011). Discutir un sistema 03 BACHILLERATO Reduccion Gauss Jordan. 28/11/2015,
de Youtube Sitio web: https://www.youtube.com/watch?v=klWAnkzOIbo
Stefan
Waner. (2007). Resumen: Álgebra de Matrices. 28/11/2015, de zweigmedia Sitio
web: http://www.zweigmedia.com/MundoReal/Summary3a.html
Nexo.
(2014). Tipos de Matrices. 28/11/2015, de Vitutor Sitio web: http://www.vitutor.com/algebra/matrices/tipos.html
AulaFácil.
(2015). Curso gratis de matrices y derivadas. 28/11/2015, de AulaFácil Sitio
web: http://www.aulafacil.com/cursos/l11067/ciencia/matematicas/matrices-y-determinantes/operaciones-con-matrices-ejercicio-8
Nexo.
(2014). Propiedades de las operaciones con matrices. 28/11/2015, de Vitutor
Sitio web: http://www.vitutor.com/algebra/matrices/operaciones.html
Nexo.
(2014). Matriz Inversa. 28/11/2015, de Vitutor Sitio web: http://www.vitutor.com/algebra/matrices/inversa.html
Nexo.
(2014). Determinantes. 28/11/2015, de Vitutor Sitio web: http://www.vitutor.com/algebra/determinantes/determinantes.html
WordPress.
(2008). Definición de Determinante. 28/11/2015, de Definición.de Sitio web: http://definicion.de/determinante/
E.
Knobloch. (2015). Determinante (matemáticas). 28/11/2015, de Wikipedia Sitio
web: https://es.wikipedia.org/wiki/Determinante_(matem%C3%A1tica)
jvcontrerasj.
(2011). Cofactores. 28/11/2015, de Youtube Sitio web: https://www.youtube.com/watch?v=jL-EbUKvgRA
Nexo.
(2014). Propiedades de los determinantes. 28/11/2015, de Vitutor Sitio web: http://www.vitutor.com/algebra/determinantes/propiedades.html
Nexo.
(2014). Regla de Cramer. 28/11/2015, de Vitutor Sitio web: http://www.vitutor.com/algebra/sistemas%20I/cramer.html
G.
Polya. (2014). Sistemas de Ecuaciones. 28/11/2015, de carmesimatematic Sitio
web: http://carmesimatematic.webcindario.com/sistemas.htm
Jagdish C. Arya & Robin W. Lardner. (2002). Matemáticas
aplicadas a la administración y a la economía. México: Pearson
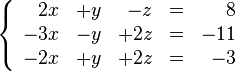


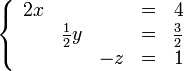

![\left [
\begin{array}{rrrr}
2 & 1 & -1 & 8 \\
-3 & -1 & 2 & -11 \\
-2 & 1 & 2 & -3
\end{array}
\right ]](https://upload.wikimedia.org/math/b/7/5/b75b0e02a527cf69e6f42dbd2fe2960f.png)
![\left [
\begin{array}{rrrr}
2 & 0 & 0 & 4 \\
0 & 1/2 & 0 & 3/2 \\
0 & 0 & -1 & 1
\end{array}
\right ]](https://upload.wikimedia.org/math/e/b/f/ebf74f6593b310153d2a6700d2f37b43.png)
![\left [
\begin{array}{rrrr}
1 & 0 & 0 & 2 \\
0 & 1 & 0 & 3 \\
0 & 0 & 1 & -1
\end{array}
\right ]](https://upload.wikimedia.org/math/d/4/0/d40cfce339ef9bb6dde8739c55d238d3.png)
![\left [ \begin{array}{cccc}
0 & 0 & 0 & a \\
\end{array} \right ]](https://upload.wikimedia.org/math/4/e/a/4ea82b742b346fc121881fd94c0d3d0c.png)