Objetivos Particular del Periodo:
El alumno comprenderá el concepto de integral definida así como su interpretación gráfica. Resolverá problemas de aplicación geométrica al mismo tiempo que resolverá problemas del entorno económico-administrativo.
El alumno aplicará técnicas adicionales para la resolución de integrales que presentan estructuras complejas asociadas con modelos y problemas del entorno económico-administrativo.
El alumno entenderá los conceptos elementales del álgebra lineal y los aplicará en problemas del ámbito económico y de gestión de negocios.
3.1 Área bajo la curva.
Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.
La integral definida se representa por 
.
.
∫ es el signo de integración.
a límite inferior de la integración.
b límite superior de la integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
https://www.youtube.com/watch?v=yc4ERt8aiQA
3.2 Teorema Fundamental del Cálculo.
(EL PRIMER TEOREMA FUNDAMENTAL DEL CÁLCULO) Sea f una función integrable en [a,b], y definimos una nueva función F en [a,b] por
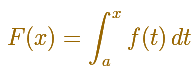
Si c pertecece a [a,b] y f es continua en c, entonces F es diferenciable en c, y
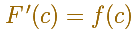
Una demostración visual bien conocida asume que la función f es continua en un entorno del punto (esta es una condición más débil, la hipótesis del teorema es más fuerte. Para una demostración analítica más rigurosa de este teorema hay que leer un buen libro de Cálculo).
Si c es un punto de (a,b), mirando la imagen podemos aceptar que
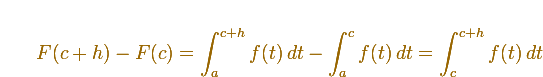
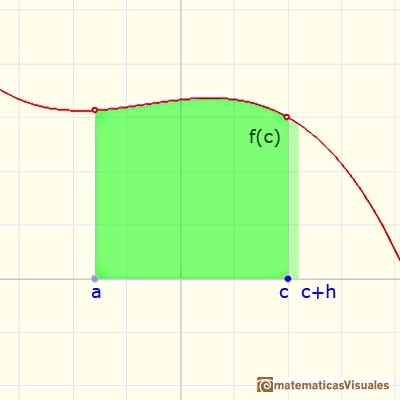
Si h es suficientemente pequeño (o podemos usar un teorema de valor intermedio, para ser más precisos)
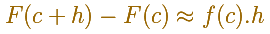
Se enuncian algunas propiedades y teoremas básicos de las integrales definidas que ayudarán a evaluarlas con más facilidad.
1) 
donde c es una constante
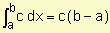donde c es una constante
2) Si f y g son integrables en [a, b] y c es una constante, entonces las siguientes propiedades son verdaderas:
(se pueden generalizar para más de dos funciones)
3) Si x está definida para x = a entonces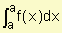 
= 0
= 0
4) Si f es integrable en [a, b] entonces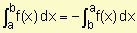 
5) Propiedad de aditividad del intervalo: si f es integrable en los dos intervalos cerrados definidos por a, b y c entonces  |  |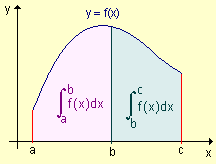
3.4 Área entre una y dos curvas.
El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo.
3.5 Aplicaciones: Excedente del consumidor y del producto, valor presente, y valor futuro.
Conclusión:
Al término de esta unidad había aprendido como obtener el área bajo una curva, el teorema fundamental del cálculo, las propiedades de la integral definida, como obtener el área entre dos curvas y como se puede aplicar en problemas que tienen que ver con los excedentes del consumidor, y del productor, el valor presente y el valor futuro.
Bibliografía:
Matefis.
(2013). Area bajo la curva I (integral definida). 26/11/2015, de Youtube Sitio
web: https://www.youtube.com/watch?v=yc4ERt8aiQA
NexoVitutor.
(2014). Integral Definida. 26/11/2015, de Vitutor Sitio web: http://www.vitutor.com/integrales/definidas/integral_definida.html
Michael
Spivak. (2011). El Teorema Fundamental del Cálculo 1. 26/11/2015, de Matemáticas
Visuales Sitio web: http://www.matematicasvisuales.com/html/analisis/ftc/ftc1.html
JulioProfe.
(2012). Teorema Fundamental del Cálculo. 26/11/2015, de Youtube Sitio web: https://www.youtube.com/watch?v=SCKpUCax5ss
ibelloj.
(2011). Área entre dos curvas. 26/11/2015, de Youtube Sitio web: https://www.youtube.com/watch?v=ljWj8QgQAa4
Celso
Soto. (2012). Excedentes Consumidor-Productor 1. 26/11/2015, de Youtube Sitio
web: https://www.youtube.com/watch?v=z1fCU5GU5fQ
No hay comentarios:
Publicar un comentario