Módulo 1. Introducción al cálculo en dos variables.

Módulo 1. Introducción al Cálculo en Dos Variables.

Objetivo Particular del Período:

El alumno comprenderá los conceptos básicos del cálculo diferencial en varias variables, así como la resolución de problemas en el entorno económico-administrativo, enfatizando aquellos del área de optimización de recursos.

1.1 Funciones en Dos Variables.

DEFINICIÓN: Sean X y Y dos conjuntos no vacíos. Una función de X en Y es una regla que se asigna a cada elemento x X una única y Y. Si una función asigna y a un x X particular, decimos que y es el valor de la función en x. Por lo general, una función se denota por letras como f, g, F o G. Denotemos con f una función determinada. El conjunto X para el cual f asigna una única y Y se denomina el dominio de la función f. A menudo se indica mediante Df . El conjunto de valores correspondiente y Y se conoce como el rango de la función y por lo regular se denota por Rf.

Ejemplo:

La función f del ejemplo 1 es el conjunto de todos los pares ordenados de la forma (P, z) tales que

 z=v25- x2 -y2

Por tanto, la grafica de f es la semiesfera en el plano x y por arriba de este cuyo centro es el origen y tiene radio 5. Esta semiesfera se muestra en la figura 1.

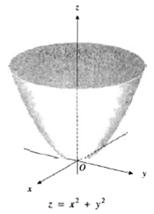
Ejemplo 2: dibuje la grafica de la función

Sol/: la grafica de f es la superficie que tiene la ecuación z=x2 +y2 . La traza de la superficie en el plano x,y se obtiene al utilizar la ecuación z=0 simultáneamente con la ecuación de la superficie. Al hacerlo resulta x2 +y2=0 la cual representa el origen. Las trazas en los planos xz y yz se obtiene al emplear las ecuaciones z=x2 +y2. Estos trazos son las parábolas z= x2 y z= y2.

1.2 Derivadas Parciales.

Sabemos que la derivada de una función de una variable en un punto nos da la pendiente de la recta tangente a la función en ese punto. Esto significa que sabemos la rapidez de crecimiento/decrecimiento de la función en ese punto.

Ahora supongamos que tenemos una función f que depende de más de una variable, por ejemplo f(x,y)=−x2+2xy−y.

Al ser una función de dos variables la gráfica es una superficie, y entonces hay infinitas direcciones entre las que estudiar el crecimiento.

Pues bien, las derivadas parciales nos indicarán también la pendiente de una recta concreta tangente a la superficie. Antes, pero, vamos a aprender a calcular derivadas parciales, ya que es una metodología a la que luego le daremos sentido.

Para calcular una derivada parcial de una función en diversas variables tenemos que derivar como siempre respecto una de las variables y mantener las demás como constantes, (como valores fijos).

En nuestro ejemplo f(x,y)=−x2+2xy−y, si queremos hacer la derivada parcial respecto x, consideramos la variable y como una constante, "un número", y entonces nos queda como derivar una función de una variable, f(x).

https://www.youtube.com/watch?v=tb00qQBYm48

1.3 Máximos y Mínimos de Funciones de Dos Variables.

Definición. Una función  tiene un máximo (mínimo) en un punto si el valor de la función en este punto es mayor (menor) que su valor en cualquier otro punto X(x,y) de algún entono de P.

Condiciones necesarias de extremo. Si una función diferenciable alcanza un extremo en el punto entonces sus derivadas parciales de primer orden en este punto son iguales a cero, o sea:

;

Los puntos en los que las derivadas parciales son iguales a cero se llaman puntos críticos o estacionarios. No todo punto crítico es un punto extremo.

Condiciones suficientes para la existencia de extremos.

(a) Caso de dos variables. Sea un punto crítico de una función  con las derivadas parciales de segundo orden continuas en P, y sea el determinante de su matriz hessiana, entonces:

Es decir, si el hessiano es positivo hay extremo (el tipo nos lo da , si es negativa máximo y si es positiva mínimo). Si el hessiano es negativo no hay extremo. Y si el hessiano es cero hay duda (que habrá que resolver por otro método)

(b) Caso de tres o más variables. Calculamos los siguientes determinantes:

; ;;...;

1. Si todos los determinantes tienen signo positivo, entonces la función tiene un mínimo en 
2. Si los determinantes tienen signo alterno (comenzando con un valor negativo ), entonces la función tiene un máximo en 
3. En cualquier otro caso hay duda.

https://www.youtube.com/watch?v=dhhmhSAOEug

1.4 Aplicaciones: Optimización de funciones de dos variables que representen gastos, ingresos o utilidad.

La derivada ordinaria dy/dx puede considerarse como la tasa de cambio de y con respecto a x. Esta interpretación a menudo es útil [por ejemplo, el ingreso marginal R(x) representa la tasa de cambio del ingreso con respecto al volumen de ventas o, aproximadamente, el cambio en el ingreso por unidad adicional vendida]. Pueden darse interpretaciones similares en el caso de las derivadas parciales. Por ejemplo, si z f(x, y), entonces,

z/

x da la tasa de cambio de z con respecto a x cuando y es constante.

EJEMPLO 1 Se lanza un nuevo producto al mercado. El volumen de ventas x se incre-menta como una función del tiempo t y depende también de la cantidad A gastada en la campaña publicitaria. Si, con t medido en meses y A en dólares,

x 200(5 e0.002A)(1 et)

calcule

x/

t y

x/

A. Evalúe estas derivadas cuando t 1 y A 400 e interprétalas.

Solución Tenemos que

x t

200(5 e0.002A)et,

A

x

0.4e0.002A(1 et)

Haciendo t 1 y A 400, obtenemos los valores

x t

200(5 e0.8)e1 335,

A

x

0.4e0.8(1 e1) 0.11

La derivada parcial

x/

t representa la tasa de incremento en el volumen de ventas con

respecto al tiempo cuando el gasto en publicidad se mantiene fijo. Por ejemplo, cuando

este gasto está fijo en $400, el volumen de ventas después de un mes (t 1) crece a una tasa instantánea de 335 por mes.

De manera similar,

x/

A da el incremento en el volumen de ventas en un instante fijo que ocurre por cada dólar adicional gastado en publicidad. En el instante t 1, cuando $400 ya se han gastado en publicidad, un dólar adicional gastado incrementará el volumen de ventas en 0.11 unidades.

https://www.youtube.com/watch?v=0sJ5IYlCTe4

Conclusión:

Lo que aprendí durante esta unidad fue que una función puede tener tener dos o más variables, aprendí que las funciones parciales son las que dependen de más de una variable y cómo definir los puntos máximos y mínimos de una función con dos variables; y por último aprendí que una función también se puede utilizar para medir los gastos, ingresos y utilidades.

Bibliografía:

Marlon Fajardo Molinares. (2009). Funciones de dos y más variables, dominio y rango, y curva de nivel . 24/11/2015, de Monografías Sitio web: http://www.monografias.com/trabajos78/funciones-dominio-rango-curva-nivel/funciones-dominio-rango-curva-nivel2.shtml

Jagdish C. Arya & Robin W. Lardner. (2002). Matemáticas aplicadas a la administración y a la economía. México: Pearson

Jaime Hernandez. (2013). Derivadas Parciales. 25/11/2015, de Sangakoo Sitio web: http://www.sangakoo.com/es/temas/derivadas-parciales

JulioProfe. (2012). Derivadas Parciales - Ejercicio 1. 25/11/2015, de Youtube Sitio web: https://www.youtube.com/watch?v=tb00qQBYm48

Salvador Vera Ballesteros. (2000). Extremos de una función de varias variables.. 25/11/2015, de Matap Sitio web: http://www.matap.uma.es/~svera/probres/pr3/pr3a3_1.html

Academatica. (2013). Máximos y mínimos funciones de dos variables. 25/11/2015, de Youtube Sitio web: https://www.youtube.com/watch?v=dhhmhSAOEug

UrbanD3. (2010). Aplicación de Derivadas: Ingreso Marginal y Utilidad Maxima. 25/11/2015, de Youtube Sitio web: https://www.youtube.com/watch?v=0sJ5IYlCTe4